Categorias

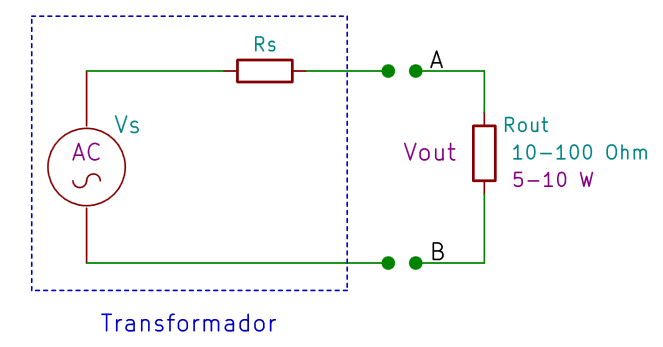
Medida de la máxima potencia de un transformador de alimentación

Figura 1: Algunos transformadores para dispositivos electràonicos con dimensiones, salidas y formas diferentes.

Los transformadores son componentes muy comunes y se encuentran en muchos dispositivos electrónicos. Hasta hace algunos años atrás eran el corazón de la alimentación de casi cualquier aparato de baja tensión, mientras en los últimos años han sido substituidos por las fuentes conmutadas, mas ligeras y pequeñas por la misma potencia. Mientras la medida de la tensión de salida de un transformador es una operación sencilla, una estimación de su potencia máxima es bastante compleja. Existen varias reglas, todas mas o menos rápidas o precisas:

Evaluación de su tamaño físico, muy dependiente de la experiencia del operador;
El peso, convertido mediante coeficientes;
Formulas que consideran su forma, las dimensiones del núcleo, el numero de espiras, la sección de los cables.

1 - El principio de medida

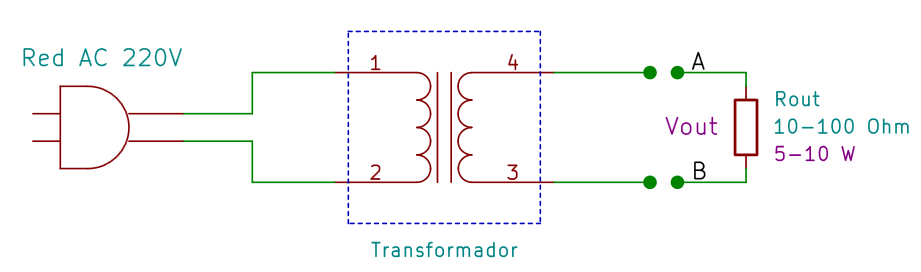
Diferentemente de todos estos métodos, el sistema de estimación de este articulo se basa en la medida de las tensiones del transformador mientras está funcionando, con sin carga y con cargo. La principal ventaja es la de medir directamente las magnitudes eléctricas desde las cuales depende la potencia suministrada por el transformador, obteniendo altos niveles de precisión.

La idea fundamental es la siguiente: el transformador está suministrando su potencia máxima cuando la tensión de salida, con carga, es un valor incluido entre el 80% y el 90% de su tensión sin carga. El porcentaje exacto n es un parámetro empírico, y varia según los modelos, pero es de todos modos posible obtener resultados bastante precisos.

2 - El proceso de medida

Figura 2: El circuito de conexión del transformador para efectuar la medida.

Para efectuar la medidad es necesario el siguiente material:

El transformador para medir;
Un multímetro que permita medir las tensiones alternadas (prácticamente todos);
Una resistencia de valor entre 10 Ω y 100 Ω, de elevada potencia (5 W o más, según el transformador);
Una clavija para conectar el transformador a la red eléctrica.

El proceso de medida es muy sencillo:

Se mide la tensión de salida sin carga V_s (que, en este caso, coincide con V_out);
Se conecta la resistencia de carga a la salida del transformador (recordamos que tiene que tener bajos valores de resistencia, entre 10 Ω y 100 Ω, y alta potencia, 5 W o más);
Se mide la tensión de salida V_out en la resistencia (es decir entre los puntos A y B);
Se calcula la potencia del transformador con la formula: 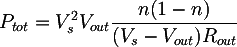$Latex: P_{tot} = V^2_s V_{out} \frac{n(1-n)}{(V_s - V_{out})R_{out}}$ donde:
- V_s es la tensión sin carga a la salida del transformador;
- V_out es la tensión medida en la resistencia de ensayo;
- R_out es el valor de la resistencia de ensayo;
- n è un valor incluido entre 0.8 y 0.9, usualmente 0,85.

También, es posible repetir la medida con otras resistencias de carga, así que será posible dibujar una curva corriente - tensión para averiguar la precisión de la medida.

3 - La resistencia de carga

La elección de la resistencia de carga es importante para la medida. En teoría cualquier valor puede ser usado. En la practica, debido a la resolución limitada de los multímetros, es oportuno elegir una resistencia pequeña, por ejemplo 10 Ω o 100 Ω, para provocar un cambio de la tensión de salida consistente. De esta manera, las incertidumbres de medida se reducen.

Además, como que tendrá que disipar mucho calor, es oportuno que la resistencia tenga potencia elevada, por ejemplo 5W o más, según el transformador; el valor puede ser calculado como: 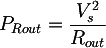$Latex: P_{Rout}= \frac{V_{s}^2}{R_{out}}$ donde:

P_Rout es la potencia de la resistencia;
V_s es la tensión de salida del transformador sin carga;
R_out es la resistencia de prueba;

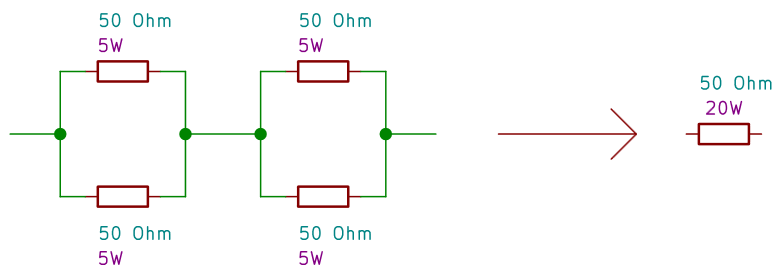
En realidad se pueden usar también resistencias con potencias mas bajas, puesto que sean conectadas al transformado solo durante pocos segundos; su calentamiento provoca primero una variación de su valor de resistencia, y luego su ruptura. Si faltan resistencias con potencia adecuada, se pueden utilizar mas resistencias en serie o paralelo para distribuir la potencia total. Un ejemplo es mostrado en la Figura 3.

Resistencias en serie y paralelo para más potencia

Figura 3: Un ejemplo de como combinar resistencias iguales en serie y paralelo para obtener una resistencia con el mismo valor pero potencia mayor.

4 - El grafico tensión-corriente

Una vez medida la tensión en la carga R_out es posible calcular la corriente subministrada por el transformador con la ley de Ohm. Si se efectúan más medidas con R_out diferentes es posible dibujar un gráfico tensión - corriente, que permite averiguar la precisión de la medida. En caso de estimación correcta, el gráfico será una recta, que confirma el comportamiento óhmico del transformador cuando no es obligado a subministrar una potencia excesiva. Si la resistencia de carga R_out fuese muy pequeña, es decir si la potencia suministrada por el transformador fuese muy alta, ocurrirían varios fenómenos físicos, como la saturación del núcleo, que volverían el comportamiento del transformado non linear; esto se traduce en una curva tensión corriente no más recta. Ademas en el caso en que haya un error en la medida (valor de R_out o V_out equivocado) la curva lo pone en evidencia pronto.

5 - Ejemplo: transformador 1

El transformador considerado tiene las siguientes características:

Tipo de salida: corriente alternada
Tensión de placa: 12 V
Tensión medida sin carga: 14,2 V
Potencia de placa: 20 VA

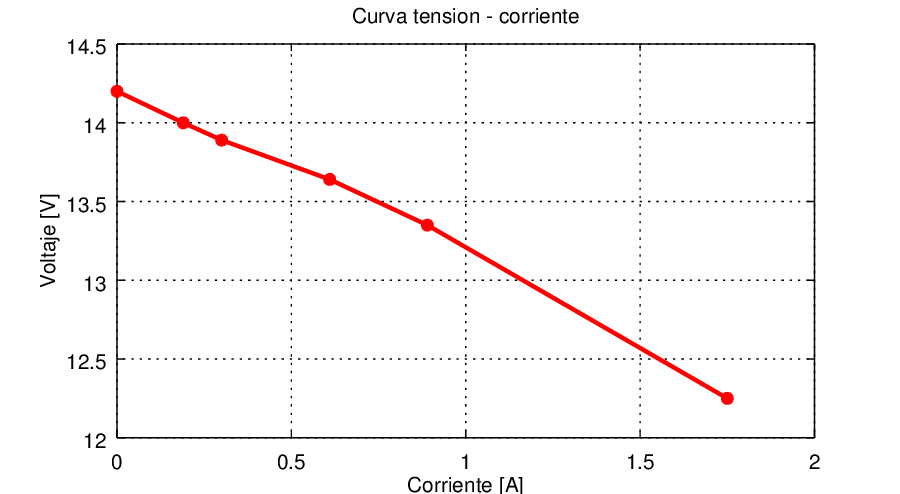
La tabla Tabella 1 montra varias medidas efectuadas con el transformador con varias resistencias de carga. Una sola seria suficiente para efectuar el calculo con la formula Formula 1, pero en este caso es posible dibujar el gráfico en Figura 5 y averiguar que el transformador tenga un comportamiento óhmico. Desde los valores de la tabla es posible notar como la estimación mejor es con un factor n=0.9, osea cuando la tensión de salida es el 90% de la sin carga.

Figura 4: El transformador 1 utilizado en este ejemplo.

Tabella 1: transformador 1
Tensión en la carga V_out	Resistencia en la carga R_out	Corriente en la carga I_out	Potencia por n=0.9 [W]	Potencia por n=0.8 [W]	Resistencia interna R_S
14,2	∞	0
14	73,7	0,19	17,24	30,64	1,05
13,89	46,1	0,30	17,64	31,36	1,03
13,64	22,4	0,61	19,73	35,08	0,92
13,35	15	0,89	19,00	33,78	0,96
12,25	7	1,75	16,29	28,95	1,11
Media:			18	32	1,04

Caracteristica tensión - corriente, transformador 1

Figura 5: La caracteristica tensión - corriente del transformador, obtenida efectuando mas medidas con resistencias de carga diferentes. Es una recta, y esto confirma el comportamiento lineal, es decir óhmico, del transformador.

6 - Ejemplo: transformador 2

El segundo transformador de ejemplo tiene las siguientes características:

Tipo de salida: corriente alternada
Tensión de placa: 14 V
Tensión medida sin carga: 15,58 V
Potencia de placa: 24 VA

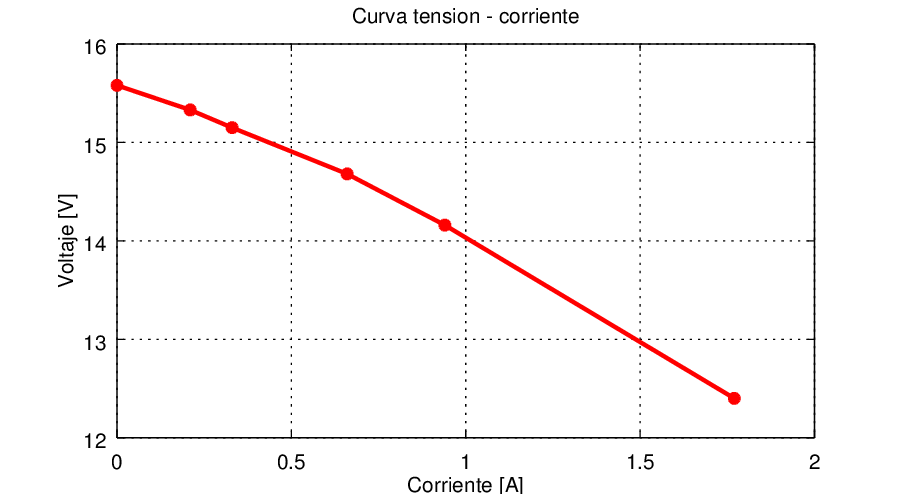
Como para el primer ejemplo, la Tabella 2 resume los resultados de las medidas efectuadas, representados en el gráfico de la Figura 5. En este caso la estimación mejor es por un factor n=0.8, es decir cuando la tensión de salida es el 80% de la sin carga.

Figura 6: El transformador 2 utilizado para este ejemplo.

Tabella 2: transformador 2
Tensión en la carga V_out	Resistencia en la carga R_out	Corriente en la carga I_out	Potencia por n=0.9 [W]	Potencia por n=0.8 [W]	Resistencia interna R_S
15,58	∞	0
15,33	73,7	0,21	18,18	32,31	1,20
15,15	46,1	0,33	16,70	29,68	1,31
14,68	22,4	0,66	15,91	28,28	1,37
14,16	15	0,94	14,52	25,82	1,50
12,4	7	1,77	12,17	21,63	1,80
Media:			15	27	1,43

Caracteristica tension-corriente, transformador 2

Figura 7: Como en el caso del transformador 1, la característica tensión - corriente confirma el comportamiento lineal y óhmico de este modelo.

7 - La teoria

En esta sección es explicada la origen de la formula de calculo de la potencia máxima. Existen varios circuitos equivalente de la puerta de salida de un transformador; entre los mas sencillos, los que lo paragonan a un normal alimentador con resistencia interna, como mostrado en la Figura 8.

Figura 8: El circuito equivalente de Thevenin de un transformador, modelado como elemento puramente lineal.

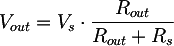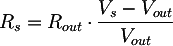
Si insertamos una resistencia R_out a la salida del transformador, creamos un divisor de tensión. La tensión de salida será: $Latex: V_{out} = V_{s} \cdot \frac{R_{out}}{R_{out} + R_{s}}$ desde esa se obtiene la resistencia interna: $Latex: R_{s} = R_{out} \cdot \frac{V_{s}-V_{out}}{V_{out}}$

Recordamos que el principio de medida asume que la potencia máxima suministrada por el transformador se obtiene cuando su tensión de salida está entre el 80% y el 90% de la tensión máxima. Definiendo del parámetro n incluido entre 0.8 y 0.9, la tensión de salida V_{out n} en correspondencia de la potencia máxima vale entonces: $Latex: P_{out} = P_{tot} \rightarrow V_{out n} = n V_{s}$ Podemos entonces encontrar la resistencia R_outn que, conectada al transformador, nos permita obtener la tensión V_outn correspondiente al suministro máximo de potencia; es decir, calculamos la carga que hace suministrar al transformador la máxima potencia. 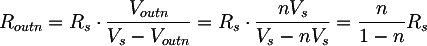Desde el divisor escrito antes se obtiene: $Latex: R_{out n} = R_{s} \cdot \frac{V_{out n}}{V_{s}-V_{out n}} = R_{s} \cdot \frac{nV_{s}} {V_{s}-nV_{s}} = \frac{n}{1-n}R_{s}$ La potencia con V_{out n} y R_{out n} será entonces: 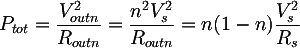$Latex: P_{tot} = \frac{V^2_{out n}}{R_{out n}} = \frac{n^2 V^2_{s}}{R_{out n}} = n(1-n) \frac{V_{s}^{2}}{R_{s}}$ Desde esta, substituyendo la expresión de R_s encontrada antes, se obtiene la formula final: $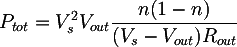Latex: P_{tot} = V^2_s V_{out} \frac{n(1-n)}{(V_s - V_{out})R_{out}}$

Tag